|
|
|
|
Click or touch headings below:
− Numbers and Sets
| Sets: |
| ℕ0 = Natural Numbers: {0,1,2,3,...} |
| ℕ1 = Natural Numbers: {1,2,3,...} |
| ℤ = Integers: {...,-3,-2,-1,0,1,2,3,...} |
| ℚ = Rational Numbers: any value expressed as a ratio a/b where a and b are any integers |
| ℝ = Real Numbers: any value that represents a quantity along a continuous line |
| ℂ = Complex Numbers: any quantity in the form a+bi where a and b are real numbers and i is the imaginary constant |
| ∅ = the Empty Set with no elements: {} |
| U = the Universal Set (all possible elements) |
| |
| Set Operators: |
| A ∈ B → A is an element of set B |
| A ∉ B → A is not an element of set B |
| A ∪ B → union of sets A and B (all elments of both) |
| A ∩ B → intersection of sets A and B (only elments in common) |
| A ⊂ B → A is a proper subset of B (A ≠ B) |
| A ⊆ B → A is a subset of B |
| 2A → power set of A (set of all subsets) |
| |
| Constants: |
| π = 3.141592653589793... ratio of circumference to diameter of circle |
| e = 2.718281828459045... Euler's number |
| i = the imaginary constant |
| φ = 1.61803398874989... golden ratio |
| |
| Operator Precedence: |
- () → Operations inside parentheses
- −x → Negative numbers [−42 = (−4)2]
- xn → Exponents
- xy → Terms like 2π [2π/4i = (2π)/(4i)]
- × / → Multiply/Divide
- + − → Add/Subtract
|
− Algebra
| Relational Symbols: |
| x = y → x is equal to y |
| x ≠ y → x is not equal to y |
| x <> y → x is not equal to y |
| x ≈ y → x is approximately equal to y |
| x > y → x is greater than y |
| x ≫ y → x is much greater than y |
| x ≥ y → x is greater than or equal to y |
| x < y → x is less than y |
| x ≪ y → x is much less than y |
| x ≤ y → x is less than or equal to y |
| x ∝ y → x is proportional to y |
| |
| Basic Algebra: |
|
|
|
|
|
| (commutative) |
| (commutative) |
| (associative) |
| (associative) |
| (distributive) |
|
|
|
|
|
|
|
|
| |
| Algebraic Equivalences: |
|
|
|
|
|
|
|
|
− Functions
| A function denoted as f(x) is a relation f between a set of inputs x and a set of permissible outputs with the property that each input is related to exactly one output. |
| |
| (even function) |
| (odd function) |
|
|
|
| (composition) |
| (non-commutative) |
| (inverse function f−1) |
| |
| Common Functions: |
| → natural logarithm (base e) |
| → exponent ex |
| → floor or nearest lesser integer |
| → ceiling or nearest greater integer |
| → real part of complex number |
| → imaginary part of complex number |
| → absolute value or distance from origin |
| → Gamma function = (x-1)! |
− Exponents and Roots
| Exponents: |
|
Exponents, also known as powers, are denoted with a superscript as in xn which is described as 'x to the power n'.
This means 'x' multiplied by itself 'n' times.
|
| (x squared) |
| (x cubed) |
|
|
|
|
|
|
|
|
|
|
|
| Roots: |
| Roots are denoted with the radical sign √ and are the result of taking fractional exponents. |
| (square root) |
|
| (cube root) |
|
| (nth root) |
|
|
|
− Logarithms
| A logarithm is denoted logn x where n is called the base and is the inverse of exponent. |
| |
|
|
| (natural log) |
| (common log) |
|
|
|
|
|
− Complex Numbers
|
Imaginary numbers are denoted xi where i is the imaginary constant and i2=−1.
Complex numbers are denoted a+bi or a−bi; where i is the imaginary constant. This is usually called rectagular form.
Complex and imaginary numbers can result from operations that have no real-number solutions such as square roots or logarithms of negative numbers.
Complex numbers are typically represented as points on a plane where the x-axis is the real part and the y-axis is imaginary. |
| |
|
|
|
|
|
|
|
| (conjugate) |
| (absolute value) |
| |
|
Alternatively, complex numbers can be represented in polar form denoted r∠θ
where r (modulus or amplitude) is the magnitude and θ (argument or phase) is the angle with respect to the real axis within the complex plane.
If z = a+bi then the polar form r∠θ is: |
| |
|
|
|
|
+ Trigonometric Functions
− Trigonometric Functions
|
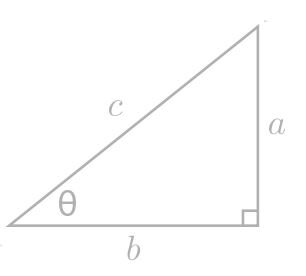
Trigonometric functions are defined as the ratios between two sides of a right triangle, denoted a, b, or c at a specific primary angle θ.
All trig functions can be referenced to a unit circle with radius 1, where the origin is defined as the center of the circle, the right triangle hypotenuse as the radius,
the base as the x-axis, and the primary angle as the angle between the x-axis and the hypotenuse.
|
| |
 |
| Basic Identities: |
| (sine;cosine) |
| (tangent;cotangent) |
| (secant;cosecant) |
| |
| Pythagorean Identities: |
| (Pythagorean Theorem) |
|
|
|
| |
| Reciprocal Identities: |
|
|
|
| |
| Quotient Identities: |
|
| |
| Inverse Functions: |
| Inverse trig functions can be denoted using any of the following forms with the example of (sin θ): |
| (asin θ) or (sin-1 θ) or (arcsin θ) |
| |
| Where: |
| ; −π/2 ≤ θ ≤ π/2 radians |
| ; 0 ≤ θ ≤ π radians |
| ; −π/2 ≤ θ ≤ π/2 radians |
| ; 0 ≤ θ ≤ π radians |
| ; 0 ≤ θ ≤ π radians |
| ; −π/2 ≤ θ ≤ π/2 radians |
| |
| Exponential Forms(i2=-1): |
| (Euler's formula) |
| (Euler's identity) |
|
|
|
|
|
|
|
|
|
|
|
|
| |
| Law of Cosines |
|
| where for any triangle: |
| a and b = adjacent sides |
| θ = angle between a and b |
| c = opposite side of angle θ |
| |
| Law of Sines |
|
| where for any triangle: |
| A, B, and C are opposite angles of sides a, b, and c |
| |
| Angles and Units: |
| 360 degrees = 2π radians = 400 grads |
| Degrees |
Radians |
Grads |
| 30 |
π/6 |
33 1/3 |
| 45 |
π/4 |
50 |
| 60 |
π/3 |
66 2/3 |
| 90 |
π/2 |
100 |
| 120 |
2π/3 |
133 1/3 |
| 135 |
3π/4 |
150 |
| 150 |
5π/6 |
166 2/3 |
| 180 |
π |
200 |
|
− Hyperbolic Functions
|
Hyperbolic functions are defined as analogs of trignometric functions except they are applied to hyperbolas instead of unit circles.
As a result, they exhibit similar identities.
Hyperbolic functions use the familiar trigonometric names with an 'h' suffix such as sinh, cosh, tanh. |
| |
| Exponential Definitions: |
|
|
|
|
|
|
| |
| Inverse Hyperbolic Functions: |
| Where: |
| ; −∞ < x < ∞ |
| ; 1 ≤ x < ∞ |
| ; 1 ≤ x < ∞ |
| ; 0 ≤ x ≤ 1 |
| ; −∞ < x < ∞ |
| ; −1 ≤ x ≤ 1 |
| |
| Definitions: |
|
|
|
|
|
|
| |
| Identities: |
|
|
|
|
|
|
|
|
|
|
|
|
| |
| Relation to Trig Functions: |
|
|
|
|
|
|
| |
|
|
|
|
|
|
− Series
| Summation: |
| Sums of discrete series are denoted using a capital Sigma (Σ), the lower expression defining the index variable and lower bound, the upper expression defining upper bound of integer values for the index. |
| (definition) |
|
|
|
|
|
|
| |
| Products: |
| Products of discrete series are denoted using a capital Pi (Π), the lower expression defining the index variable and lower bound, the upper expression defining upper bound of integer values for the index. |
| (definition) |
| (factorial) |
| |
| |
| |
| Taylor Series: |
|
The Taylor Series is a method that allows any differentiable function to be expressed as a series.
In many cases the Taylor series can have an infinite number of terms and the function can only be approximated via calculation.
Expressed as a sum, the Taylor series is denoted:
|
|
| | where n! denotes the factorial of n and ƒ(n)(a) denotes the nth derivative of function ƒ evaluated at point a. |
| |
| Maclaurin Series: |
|
The Maclaurin Series is a special case of the Taylor Series that is evaluated at zero where the function has a solution at zero.
This case significantly simplifies the construction of the polynomial series.
A Maclaurin series can be constructed for many functions, which an infinite summation in the form:
|
|
| | where n! denotes the factorial of n and ƒ{n}(0) denotes the nth derivative of function ƒ evaluated at 0. |
| |
| Common Maclaurin Series: |
| for |x| < 1 (geometric series) |
|
|
|
|
|
|
|
− Statistics
| Standard Deviation: |
|
In statistics or probability theory, standard deviation represented by lower case sigma (σ), shows how much variation exists in a data set from the average or mean value.
A small standard deviation indicates that the data points tend to be very close to the mean; a large standard deviation indicates that the data points are spread out over a wide range.
|
|
|
|
|
σ = std. deviation of population S = std. deviation of sample xi = sample variable μ = arithmetic mean of population X = arithmetic mean of sample SE = Standard Error |
| Normal Distribution: |
|
|
| Log-Normal Distribution: |
|
|
σ = std. deviation x = random variable μ = population mean CDF = Cumulative Distribution Function PDF = Probability Distribution Function |
− Calculus
| Limits: |
|
A limit is the output value that a function or sequence approaches, or converges to, as the input approaches some specific value.
Limits are most useful when the input value approaches infinity, or approaches a divide-by-zero, and the limit is a finite quantity.
|
| |
| This example shows a limit when approaching a divide-by-zero condition: |
|
| This example shows a limit when the input value approaches infinity: |
|
| Limit of sum/difference: |
|
| Limit of product: |
|
| Limit of quotient: |
|
| Multiplication by constant: |
|
| |
| Derivatives: |
|
A derivative can be described as the slope of a point on a continuous function.
Derivatives can represent instantaneous rates of change in any quantity that is described by a continuous function.
For any function f(x)=y derivative is defined using the limit of the ratio of the change in y over the change in x (Δy/Δx) as Δx approaches zero.
|
| |
| The derivative of the function f(x) at the point x0 is denoted: |
|
| Second derivative: |
|
| Derivative of Sum/Difference: |
|
| Derivative of Product: |
|
| Derivative of Quotient: |
|
| Chain Rule: |
|
| |
| Integrals: |
|
An integral can be described as the area under a continuous curve on a graph.
Integrals can represent the sum of all values over any quantity that is described by a continuous function.
The integral is the inverse function of the derivative (antiderivative) as described by the Fundamental Theorem of Calculus.
|
| |
| Where: F'(x) = f(x) |
| - for a continuous function f(x), the indefinite integral is denoted: |
|
| - for a continuous function f(x) over interval [a,b], the definite integral is denoted: |
|
| |
| Fundamental Theorem of Calculus: |
|
|
| |
| Conventions: |
|
|
| If a ≤ b ≤ c : |
|
| |
| Integral of Sum/Difference: |
|
| Multiplication by a constant: |
|
| |
− Table of Derivatives
| Basics: |
|
|
|
|
|
|
|
| Trigonometric: |
|
|
|
|
|
|
| Inverse Trigonometric: |
|
|
|
|
|
|
| Hyperbolic: |
|
|
|
|
|
|
| Inverse Hyperbolic: |
|
|
|
|
|
|
− Table of Integrals
| (Constant of integration ...+C assumed) |
| Basics: |
|
|
|
|
|
| Rational Functions: |
|
|
|
|
|
|
|
| Exponential: |
|
|
|
|
| Logarithmic: |
|
|
|
|
| Trigonometric: |
|
|
|
|
|
|
| Inverse Trigonometric: |
|
|
|
| Hyperbolic: |
|
|
|
|
|
|
| Inverse Hyperbolic: |
|
|
|
|
|
|